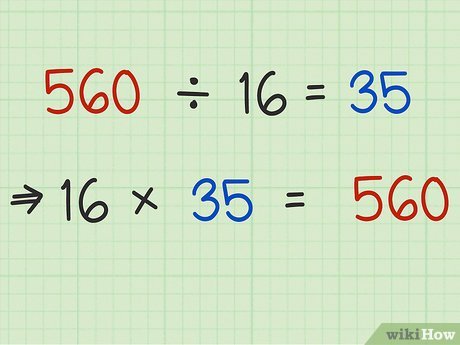There were Greek and Roman mathematicians before Euclid.
Both arithmetic (the study of “multitude,” or discrete amount) and geometry (the study of shapes and their relationships) have their roots in practical applications, and the Greeks separated them as separate branches of mathematics (the study of “magnitude,” or continuous number). In light of the fact that periodic flooding along the Nile required the Egyptians to redraw property boundaries, Proclus attributes the origin of geometry (which means “measure of land”) to ancient Egyptian surveying practises. And it was Phoenician traders who pushed the boundaries of mathematics forward. Proclus’ narrative, published in the fifth century CE, depends on the work of earlier philosophers such as Herodotus (mid-fifth century BCE) and Eudemus (an Aristotelian follower), both of whom precede his time (late 4th century BCE). Percentages and other mathematical methods are covered in detail on their site, so if you’re having trouble with them, you should check it out.
Determine 50% of 3400.
To begin, the first step’s output is the value 3400.
Second, let’s pretend the unknown number is x.
Third, take the result of 3400 = 100% as the output value.
Fourth, in the same vein, x is equal to 0.5.
Fifth, by dividing the pair of easy equations, we arrived at the following formula:
3400 = 100% (1). (1).
x = 50% (2). (2).
(3400%)/(x%) = 100/50
The following equation is the result of Step 6’s balancing of the two sides:
x%/3400% = 50/3400
By further simplifying the above-obtained equation, we can determine the answer to Step 7: 50% of 3400 is.
x = 1700%
So, if we divide 3400 by 0.5, we get 1700. [source:] percentage.wiki
Since there is so little evidence of early Greek applied mathematics, testing this hypothesis is challenging but not impossible (roughly, the 8th through the 4th century BCE). Some stone tablets include numbers that seem to be similar in concept to the familiar Roman numerals. Herodotus probably knew the abacus as a tool for arithmetic in both Greece and Egypt, since there are approximately a dozen stone abacuses that date back to the fifth and fourth century BCE. 70 plethra (one plethron equals 100 feet) was commonly used as the diagonal of a square with sides of 50 plethra when surveying new cities in Greek colonies in the sixth and fifth centuries BC. In reality, the diagonal of the square is 50Square root of2 plethra, so this is equivalent to using 7/5 (or 1.4) as an estimate for Square root of2, which is now known to equal 1.414…. Historians disagree on how the engineer Eupalinus of Megara managed to bore an aqueduct through a mountain on the island of Samos in the sixth century BCE. It seems from Plato’s Laws that the Greeks might have learned a thing or two from the Egyptians about how to best instruct their young in mathematics and geometry by having them solve problems with immediate practical applications.
These speculations regarding the nature of early Greek practical mathematics are supported by the arithmetic problems recorded in Ptolemaic Egyptian papyri (beginning in the third century BCE) and the geometric guides by Heron of Alexandria (1st century CE). The ancient Egyptians and the Mesopotamians were the original developers of this practise that the Greeks adopted. The Greeks undoubtedly drew inspiration from far earlier cultures.
A common argument for the Greeks’ status as the reputed “creators of mathematics” is that they were the first to place an emphasis on theory in their mathematical practise. Consequently, mathematical propositions are universal and may be shown to be right. Examples of Mesopotamian mathematical innovation include techniques for determining whether or not the equation a2 + b2 = c2 holds for a given collection of whole integers (e.g., 3, 4, 5; 5, 12, 13; or 119, 120, 169). For each pair of whole numbers p and q, even or odd, the Greeks developed a formula for generating the sequence a = (p2 + q2)/2, b = (pq)/2, and c = (p2 + q2)/2, now often referred to as the Pythagorean triples. For Pythagorean triples, these numbers meet the criteria that Euclid lays forth in Book X of the Elements. The Greeks established this result as part of a larger theory describing the properties of two-dimensional geometric shapes (Euclid proves it twice, once in Book I, Proposition 47, and once in Book VI, Proposition 31). Mesopotamians apparently understood that right triangles had side lengths that are multiples of the three integers a, b, and c.
Despite the widespread acceptance of Euclid’s The Elements (written about 300 BCE) as the foundation of theoretical geometry, the shift from applied to theoretical mathematics did not occur until the fifth century BCE. Following in the footsteps of Pythagoras of Samos (late 6th century) and Hippocrates of Chios (late 5th century), other Pythagoreans, such as Archytas of Tarentum, Theaetetus of Athens, and Eudoxus of Cnidus, developed new ideas and techniques in the theoretical form of geometry (4th century). Because none of their works have survived, what we know about them comes from the accounts of other authors. Although this scrap of evidence shows how much Euclid depended on them, it doesn’t tell us anything about what inspired his research.
We examine the background of this theoretical shift and its implications. It has been suggested that the discovery of irrational numbers was the catalyst for this change. Among the earliest Pythagoreans, the belief that “all things are number” was a central tenet. In spite of the fact that the Greek word for number, arithmos, typically only refers to whole numbers and, in certain instances, to ordinary fractions, this may be interpreted to suggest that every geometric measure has a corresponding number (that is, some whole number or fraction; in modern terminology, rational number). This is simply assumed in everyday discourse, like when the length of a line is stated as a whole number of feet plus a fraction of a foot. With that said, the lines that make up the square’s sides and diagonal are an exception. (For instance, it can be shown that the ratio of two whole integers is always an even number since the ratio of the side ratio to the diagonal ratio is always an even number. It is self-evidently impossible for this to happen, since every fraction may be written as a ratio of two whole numbers that share no components. For this reason, in geometry, the length of a side and the length of a diagonal cannot both be multiples of the same set of (different) whole integers. The Greeks used the term “incommensurable” to describe such extreme differences in scale. (Contrary to the ancient Greeks, modern mathematicians often use the word “number” to refer to irrational numbers such as the Square Root of 2.)
Some later writers, such as Pappus of Alexandria (4th century CE), say that it was discovered inside the Pythagorean school in the 5th century BCE, but by the time of Plato, it was common knowledge. This fact, known from at least 400 BCE, was already common knowledge. Lines corresponding to the square root of 3, the square root of 5, and other square roots are not comparable to a standard unit of length. Theaetetus, a friend of Plato’s, is frequently credited with discovering the geometric analogue of the famous “when p is not a rational square number, the square root of p is irrational” theorem. Theaetetus and Eudoxus set the groundwork for the rest of their students to build upon, and Proposition 115 of Book X, Section II of the Elements is proof of this.
Whatever assumptions were made in actual practise, the discovery of irrationals undoubtedly transformed the emphasis of early mathematical inquiry. The irrationals proved that geometry needs more than just numbers. Once fundamental mathematical assumptions, such as the comparability of all lines, were shown to be wrong, it was possible that any other assumption may be wrong as well. All mathematical claims have to have some kind of minimal justification. What’s more, it was critical to define what characteristics a line of reasoning must have in order to be labelled a proof. Hippocrates of Chios and his contemporaries obviously began compiling geometric results into textbooks titled “elements” before his death in the fifth century BCE (meaning “fundamental outcomes” of geometry). They would be used as sources by Euclid, a century later, when he was creating his complete textbook.
Early mathematicians faced stiff competition from the likes of the pre-Socratic philosophers of Ionia and Italy and the Sophists of Athens. In the fifth century BCE, the Greek philosopher Parmenides questioned the very foundations of knowledge by claiming that only unchanging objects could have true existence. However, Heracleitus (about 500 BCE) argued that the constancy of our senses is an illusion caused by a balance of competing forces. A discussion ensued, with the words “knowledge” and “evidence” at the centre.
A lot of arguments revolved on mathematical details. The Pythagoreans, followed by Plato, utilised the mathematical certainty as a model for deducing truths in other disciplines, including politics and ethics. However, there were also many who objected on the basis of logical fallacies in mathematical reasoning. Zeno of Elea, a Greek philosopher who lived in the fifth century B.C.E., has been credited with creating paradoxes involving the concepts of motion and number. When we suppose that a line may be cut indefinitely at right angles, we obtain either a group of points with no length (in which case the sum of an infinite number of such points is zero) or a collection of very short lines (in which case the sum is infinite). The specified line’s length must be both zero and satisfy this practical criterion. Atomist philosophers like Democritus in the fifth century BCE suggested that the world is made up of infinitesimally tiny components called “atoms” in an attempt to explain away such paradoxes (from the Greek atomon, meaning “indivisible”). However, the concept of incommensurable lines non geometry contradicted this strategy, since it required measuring all lines in atoms. Whether a tangent meets a circle at a point or a line is not always clear; not even the Sophist Protagoras and Democritus could agree on this. Neither Antiphon, a Socratic philosopher from the fifth century BCE, nor Bryson, a Socratic philosopher from the fourth century BCE, underestimated the difficulty of discovering an equation between a circle and any of the polygons that may be formed within it.
The pre-Socratics played a crucial role because they identified issues with not just general concepts like “infinitely numerous” and “infinitely little,” but also with more basic ones like “existence” and “evidence.” While it’s impossible to tell for sure how these philosophical questions affected mathematicians’ technical research, we can say that they became less confident in making sweeping claims about the scope of mathematics as a whole.
Since the sources are contradictory and never make it obvious how the mathematicians answered to the questions that were addressed, it is hard to draw any definite conclusions regarding the anticipated impacts of such features. Greek mathematics may be identified by its careful scrutiny of primary assumptions and emphasis on robust proofs. While it is impossible to provide a complete explanation for these shifts, we may look to the unique conditions of the early Greek tradition, including its technological developments and cultural milieu, to begin to piece together their origins.